Chapter 1: Kinetic Terms and Their Implications

In the previous discussion, I examined potential kinetic terms to integrate into our physical framework. We have already dismissed one kinetic term due to its overly simplistic reduction of the equation structure we aimed to achieve. This particular term resulted in solutions with negative energy. Moreover, the excluded kinetic term compelled our representation to mimic four distinct spin-zero particles, which was not our intention. We still have two kinetic terms left to consider, leading us to the conclusion that the most comprehensive kinetic term is a linear combination of these two. The coefficients associated with each term are designated as 'a' and 'b'.

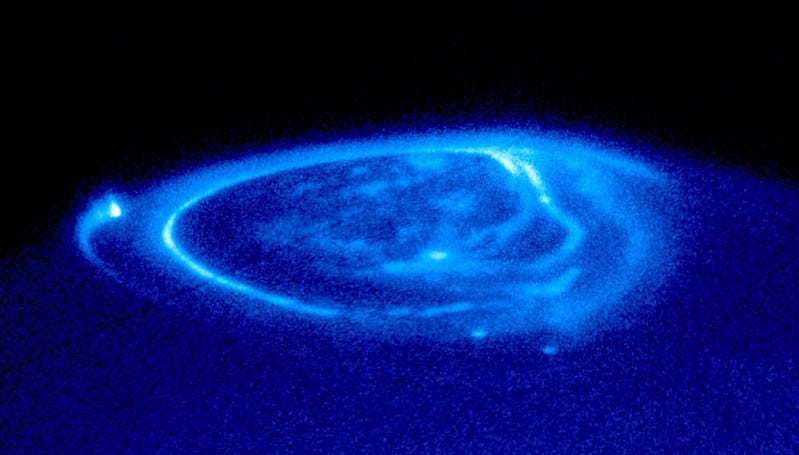
The second kinetic term plays a crucial role in ensuring that our vector does not behave like four scalars. This is achieved by contracting it with a partial derivative term, which transforms like a vector. If the vector field A did not conform to this transformation, we would encounter significant issues. Now that we have established that the vector field A must transform within a four-dimensional framework, we need to impose a constraint to simplify it to a three-dimensional model. The nature of this constraint will become evident when we derive the equations of motion from this Lagrangian. By contracting the results from the Euler-Lagrange equations with a partial derivative, we discover that

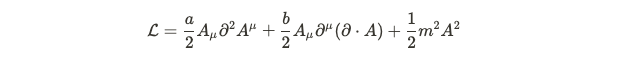
A constraint is already apparent in this equation. By setting a = -b, we enforce that the divergence of A equals zero, which is essential for reducing the system to three degrees of freedom. Substituting this back into the original Lagrangian leads us to recover standard electrodynamics, now incorporating a mass term. Further algebraic manipulation confirms that the energy-momentum tensor linked with this Lagrangian is indeed positive definite.

Massless Spin-1 Particles

When considering massless scenarios, we find only two degrees of freedom. The massless Lagrangian for a spin-1 particle is analogous to that of a photon but is applicable to various particle types. A common method to count the degrees of freedom involves examining symmetries that preserve the Lagrangian's form and establishing conditions that effectively constrain A, thereby reducing our degrees of freedom.

As we will observe, these two degrees of freedom align with representation theory principles. In the absence of mass, an irreducible representation possesses only two independent states. One approach to reduce these degrees of freedom is through the concept of gauge symmetry. Gauge symmetry involves transforming the underlying field without altering the physical laws governing the system. This differs from coordinate system transformations within the Poincaré group, where the intrinsic field remains unchanged. For instance, in Lorentz transformations, we adjust the coordinates while keeping the field A, which is a tensor, intact.

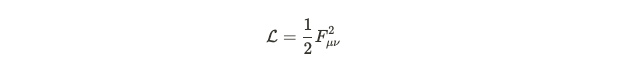
In contrast, a gauge transformation modifies the physical field according to the following rule, where Alpha is a scalar function. It is straightforward to demonstrate that this transformation does not affect the Lagrangian. Since the Lagrangian encapsulates all relevant information about a given system, this alteration is non-physical and can thus be treated as a symmetry, similar to a Lorentz transformation.

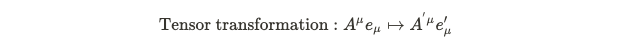
This property allows us to eliminate one degree of freedom, as the divergence of A must be zero.

The first video, "Degrees of Freedom | Classical Mechanics | LetThereBeMath," provides an insightful overview of the concept of degrees of freedom within classical mechanics, essential for understanding Lagrangian dynamics.

The second video titled "Lagrangian Mechanics II: Degrees of Freedom, Generalized Coordinates and a Cylinder" delves deeper into the principles of Lagrangian mechanics, emphasizing degrees of freedom and generalized coordinates.

References

[1] Schwartz, Matthew D. Quantum Field Theory and the Standard Model. ISBN: 8601406905047