Exploring the Connection Between Brownian Motion and Heat Equations
Written on
Chapter 1: Understanding Heat Distribution
Brownian motion, a fascinating aspect of random movement, holds a significant yet often overlooked relationship with heat distribution. This connection is crucial for those working within the realm of mathematics and physics, despite being relatively unfamiliar to the general public.
This article aims to provide a straightforward overview of how Brownian motion correlates with the heat equation, without delving into complex technicalities. For those seeking a more detailed technical analysis of the heat equation, Cantor's Paradise offers an informative resource:
The Heat Equation, explained: Your first PDE. Bonus: Fourier series.
For a broader understanding of Brownian motion itself, you can refer to my previous article, which includes a wealth of information and visuals:
A Few Strange Facts About Brownian Motion: Randomness can be unintuitive.
Let’s dive in.
How Heat Distributes
We begin with a fundamental concept often encountered in introductory differential equations: the heat equation. This partial differential equation yields a solution that is a function, typically denoted as u(x,t), representing the temperature at position x at time t. Initially, u(x, 0) indicates the starting distribution of heat.
To illustrate, imagine a one-dimensional rod fixed at both ends at 0 degrees, with the middle heated to 100 degrees.
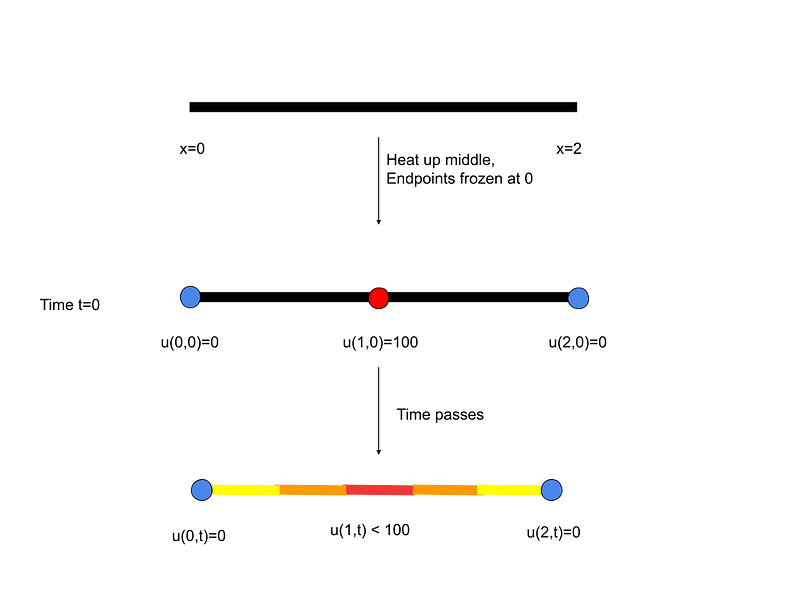
This scenario presents a mathematical paradox, as it's impossible to keep the ends at 0 degrees while the center is at 100 degrees. As time passes, the solution u(x,t) shows how the heat spreads, reflecting the expected outcome: the center remains the hottest, with temperatures gradually decreasing toward the endpoints. Ultimately, as time approaches infinity, the entire rod cools down to 0 degrees. If the endpoints were maintained at 50 degrees, the rod would stabilize at a constant temperature of 50 degrees.
An intriguing characteristic of the heat equation is its tendency to yield a smooth solution, irrespective of the initial conditions. Although u(x,0) displays a discontinuity at x=1 (100 degrees at the center versus 0 elsewhere), the solution u(x,t) remains continuous for all t>0. This indicates that heat disperses immediately across the medium, a phenomenon that stems from the idealized nature of the heat equation.
Next, consider extending this concept to two dimensions across the xy-plane. If we heat the origin to 1 while keeping all other points at 0, the solution u(x,y,t) represents the temperature at any point (x,y) at time t.
As time progresses, the heat radiates outward:
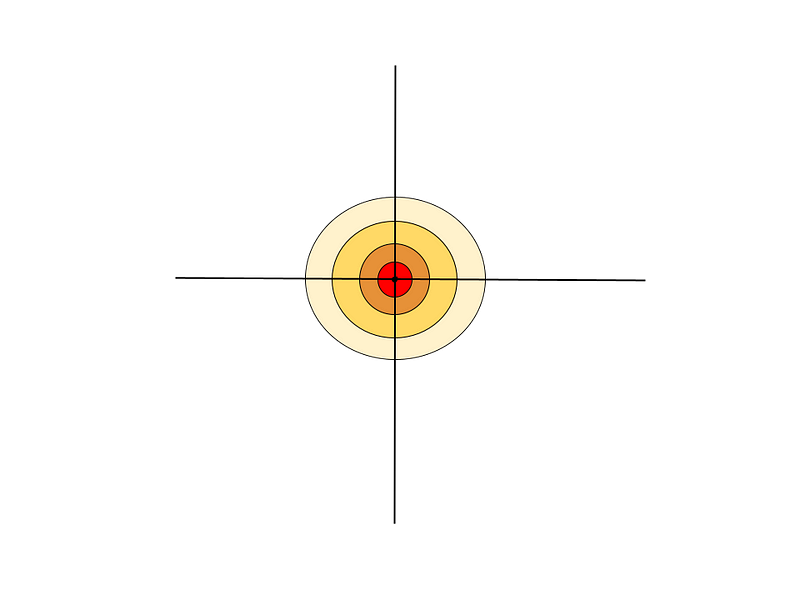
The temperature at the origin declines over time, with heat becoming more uniformly distributed across the area. This peculiar behavior highlights that heat, initially concentrated at (0,0) at time t=0, instantaneously disperses throughout the plane for any t>0, a stark contrast to the behavior of the wave equation.
Chapter 2: Introducing Brownian Motion
Brownian motion in two dimensions can be conceptualized by observing a particle starting at (0,0) and moving randomly in any direction.

This process is inherently probabilistic, leading us to consider the probability distribution of the particle's position over time. Denote this distribution as p(x,y,t), representing the likelihood of locating the particle at coordinates (x,y) at time t. Initially, p(0,0,0)=1, since the particle starts at the origin. At t=0, p(x,y,0)=0 for all other points, confirming the particle's initial position.
Once the particle is released (t>0), it could be found anywhere, though it remains more likely to be near the starting point. The probability decreases exponentially with distance from (0,0). For instance, at t=1, the particle's distribution can be visualized as follows:
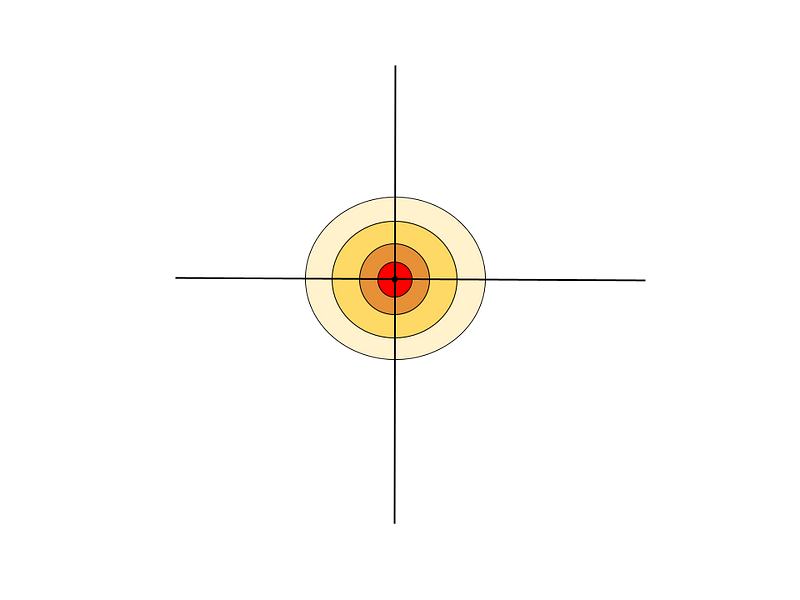
Astonishingly, this probability distribution aligns perfectly with the solution to the heat equation where 1 unit of temperature is applied at (0,0) and 0 elsewhere. This means that p(x,y,t) is equal to u(x,y,t), highlighting a remarkable connection between random motion and heat distribution.
Conclusions
As mentioned, this fundamental insight into Brownian motion may not seem profound at first glance. However, it reveals intriguing implications. For instance, we previously noted that heat disperses instantly across the xy-plane after t=0. Consequently, it’s plausible to find a randomly moving particle far from its origin even at very small time intervals.
Thus, we can appreciate how randomness is intricately linked to heat distribution.