Exploring Lie Algebras and Angular Momentum in Quantum Mechanics
Written on
Chapter 1: Understanding Angular Momentum in Quantum Physics
In classical mechanics, when you increase the spin of an object, its angular momentum grows gradually. In contrast, quantum mechanics presents a different scenario. The angular momentum of a quantum particle is quantized, meaning it can only assume certain discrete values rather than any arbitrary number. This quantization reveals an interesting symmetry that I aim to discuss in this post.

We can illustrate symmetry groups within physics using concepts known as ‘roots’ and ‘weights’. These vectors convey critical information about the representation of a Lie group. The angular momentum structure is intimately linked to a specific group known as SU(2). This group consists of 2x2 matrices that have a determinant of 1, ensuring they do not scale vectors during transformation. Additionally, these matrices must be unitary.
In matrix theory, the Hermitian conjugate of a matrix is obtained by transposing it (flipping it across its diagonal) and then taking the complex conjugate of its elements. For a matrix to qualify as unitary, its Hermitian conjugate must also serve as its inverse. This relationship can be expressed mathematically, with the dagger symbol indicating the Hermitian of a matrix.
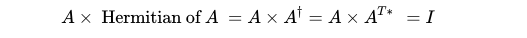
The SU(2) matrix group is also classified as a Lie group due to its properties as a smooth manifold—each matrix can be viewed as a point in a four-dimensional space.
Section 1.1: The Lie Algebra of SU(2)
The SU(2) group can be perceived as a manifold itself. However, like any manifold, we can derive the tangent space at specific points and explore the group structure of this tangent space. Confusingly, the tangent space of the Lie group SU(2) is denoted by L(SU(2)) and is referred to as a Lie algebra. A matrix belongs to the Lie algebra of SU(2) if it is anti-Hermitian—its Hermitian conjugate must equal the matrix multiplied by -1.
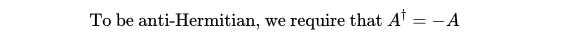
With any group, we often seek a 'basis' made up of fundamental building blocks to generate all group elements. In this section, we will explore how this idea relates to the representations of the Lie algebra L(SU(2)) and its connection to ladder operators in angular momentum. To start, we will identify a logical basis for L(SU(2)). We already know that the Pauli Sigma matrices are Hermitian. When multiplied by the complex number -i, they yield an anti-Hermitian basis from which we can construct L(SU(2)).
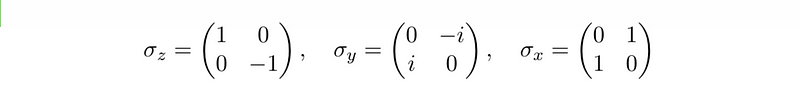
The basis described above offers a solid framework to derive elements of L(SU(2)). Typically, we build this framework using real numbers, meaning that the coefficients associated with this basis must be real. This can be expressed as LR(SU(2)), explicitly indicating that we are working over the field of real numbers.
Alternatively, we can adopt a different basis with advantageous properties. First, we will complexify our basis for L(SU(2)), allowing for complex coefficients. We denote this complexification as LC(SU(2)). This basis is referred to as the Cartan-Weyl basis, represented by the three matrices below.
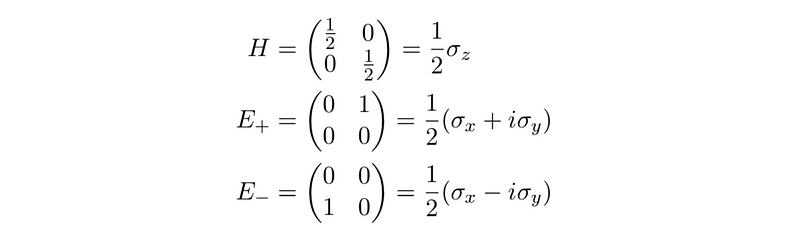
These matrices exhibit intriguing relationships with one another. When analyzing the structure of matrix groups, examining how matrices commute often reveals surprising insights about their interactions. For instance, the commutator of two matrices A and B is denoted by [A, B] = AB - BA. Below, you can see the commutators of these matrices, and you may verify their correctness by calculation.
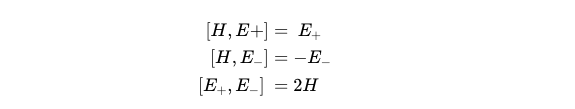
Notably, when we commute these matrices with each other, they remain within the same set. This behavior is not always guaranteed with three matrices, yet it holds true in this case. Specifically, commuting the matrix H with E+ yields a positive result, while commuting it with E- results in a negative one. Here, the matrix H acts like a ‘scaling’ matrix, with E+ and E- serving as eigenvectors since their directions remain unchanged.
Section 1.2: Complexification in Lie Algebras
Previously, we expressed L(SU(2)) using complex matrices with real vector coefficients. Alternatively, we can represent this using real matrices but with complex coefficients, a method known as complexified Lie algebra. This approach is often more manageable in various contexts.
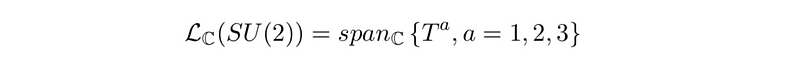
We can expand a general Lie algebra element in terms of the basis and its components, where X_H, X+, and X- represent the complex-valued components.
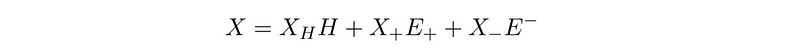
The condition that X is anti-Hermitian imposes specific requirements on these coefficients.
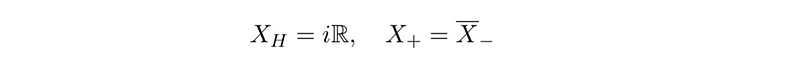
We will later find that H possesses unique characteristics, leading us to refer to it as the 'Cartan' element.
Chapter 2: The Adjoint Map and Representation Theory
The commutators we've calculated allow us to adopt a different perspective through a construct known as the adjoint map, or ‘Ad’ map. This map arises when you commute a matrix with a specific matrix. For instance, Ad_H denotes the induced map that transforms matrix A to [H, A]. Similarly, Ad_J transforms any matrix A to [J, A]. Reframing our discussion in terms of ‘maps’ can often facilitate understanding, as there is considerable mathematical machinery available for this purpose.
From our previous discussions, we understand that the Ad map from matrix H has the following properties.
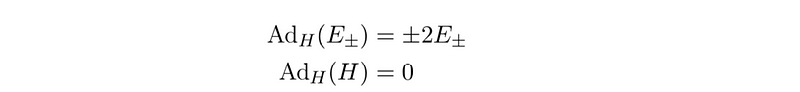
This allows us to regard the Cartan basis as an eigenbasis of Ad_H, with eigenvalues 0, ±2. These relationships parallel the ladder operators used in quantum mechanics for representing angular momentum states. Our next objective is to analyze this problem through the lens of representation theory, aiming to devise a finite N-dimensional representation of this Lie group, which will be explored in a forthcoming post.
Section 2.1: Roots and Weights in Representation Theory
In representation theory, roots and weights serve to describe the eigenvalues linked with a specific basis element in our Lie algebra and its corresponding representation. Previously, we established that the Cartan basis diagonalizes the map Ad(H), yielding eigenvalues of 0, ±2. We will refer to these as the roots of the system. Let us now consider a finite representation of L(SU(2)) against the backdrop of the Cartan basis. Recall that a finite representation is one where the vector space we are acting on is finite. We will simplify our analysis by assuming that our Cartan element H has a diagonalizable representation. This implies that when we map H into representation space as a dim R × dim R matrix, R(H) is diagonalizable.
In other words, there exists a basis set of eigenvectors such that
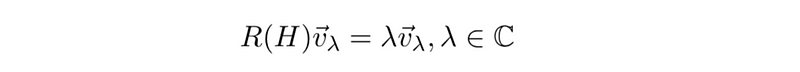
We find that these eigenvectors exist in a complexified space. Furthermore, this set of eigenvectors should also function as a basis for our representation space V. The preservation of the Lie bracket by Lie algebras proves advantageous here. Given a known weight, we can move up or down to yield a new eigenvector R(E±) with a new weight ±2.
The first video provides a comprehensive understanding of the mathematical structure underlying quantum theory, specifically focusing on Lie groups and Lie algebras.
The second video delves into particle physics, offering insights into Lie groups and Lie algebras, providing a broader context for their applications.
References
[1] Introduction to Lie Algebras, Karin Erdmann, Mark J. Wildon. Springer.