Exploring a Challenging Probability Problem from Cambridge University
Written on
Chapter 1: Introduction to the Problem
In this section, we will delve into a thought-provoking probability question sourced from the Cambridge University entrance exams. This specific question is part of the rigorous Sixth Term Examination Papers (STEP), which are utilized to assess high school students for entry into the esteemed Mathematics Tripos at Cambridge. The problem may seem straightforward at first glance, as it revolves around fundamental probability concepts. However, solving it proves to be quite demanding. I will first present the problem so that those interested can attempt it independently before I share my solution approach.

Chapter 1.1: The Problem Statement
The task may sound somewhat trivial due to its nature of assigning random scores on exam papers, yet it poses an intriguing mathematical challenge. Here’s the essence of the problem:

When approaching this problem, it's crucial to remember that these questions are structured to lead you through progressive solutions. Keep this in mind as you navigate through the various components, as they are not all straightforward.
Chapter 1.2: Analyzing Two Papers
The first part of the question involves two examination papers. We need to examine a situation where the total score exceeds the highest score for a single paper (m < n ? 2m).
To determine the combinations resulting in n marks, we can start with the maximum score of m for Paper 1, which would imply that Paper 2 scores n-m. By incrementally lowering the score of Paper 1 by 1 and correspondingly increasing Paper 2's score, we can establish a pattern: Paper 1 could score m - 1 while Paper 2 could score n-m + 1, continuing this until we reach a point where Paper 1’s score is n-m and Paper 2's is m, which is the reverse of our initial setup.
Each specific score has a probability of 1/(m+1), and since both papers are independent, the probability of any unique score combination is 1/(m+1)².
Next, we calculate the unique ordered pairs of scores. The Paper 1 scores range from m down to n-m, yielding a total of 2m - n + 1 unique combinations. Consequently, the overall probability for this scenario can be derived.
We are also tasked with determining the outcome when the total score is less than or equal to the maximum score of a single paper (0 ? n ? m). This situation is simpler, and we can start with an assumption of n for Paper 1 and 0 for Paper 2, incrementally adjusting the scores until Paper 1 reaches 0 and Paper 2 reaches n. This results in n + 1 unique ordered score pairs, each with a probability of 1/(m+1)².
Chapter 2: Addressing Three Papers
As we extend our analysis to three papers, the complexity increases. We must first evaluate cases where the total score exceeds the highest possible score for a single paper but remains within the range of two papers (m < n ? 2m).
Let’s denote the total scores for the first two papers as k, with the score for the third paper being n-k. Given our earlier condition, we know that the maximum k can be is 2m and the minimum is n-m. Since the total score from the first two papers dictates the third paper's score, we only need to determine the total probabilities for various k occurrences.
For every total mark k from the first two papers, we can apply the previously derived formulas to compute the probabilities, depending on whether k is more than the maximum for one paper.
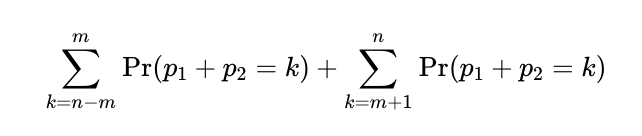
The probability of obtaining scores k from the first two papers must be multiplied by 1/(m+1) to account for the probability of the third paper scoring n-k. This leads us to a simplified equation that can be tackled using the sum of consecutive integers.
In conclusion, we will also derive results for n when considering three papers. First, when n does not exceed the total possible score for one paper (0 ? n ? m), the sum k for the first two papers can be anything from 0 to n, leading us to a straightforward solution.
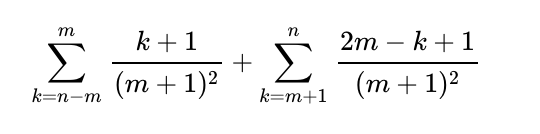
The final case, where 2m < n ? 3m, introduces a new aspect since we hadn’t addressed this in previous parts. However, we can cleverly reframe the problem, considering it from a different angle, leading to another insightful calculation.
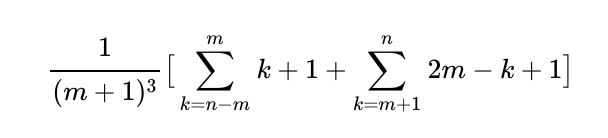
What are your thoughts on this complex problem and its solutions? Have you arrived at a different conclusion or approached it uniquely? I welcome your comments and insights.
In this video, we explore a challenging probability question from the Cambridge STEP papers and break down the methodology for tackling it.
This video discusses solving a question from the Cambridge Entrance Exam, offering tips and strategies for approaching similar problems.