Discovering Pythagorean Triples: The Case of 19
Written on
Understanding Pythagorean Triples
A Pythagorean triple consists of three non-zero integers (a, b, c) that satisfy the equation a² + b² = c². Essentially, these integers represent the lengths of the sides of a right triangle. For this particular puzzle, we aim to identify a Pythagorean triple where 19 is the smallest value, and both b and c must also be integers.
Typically, Pythagorean problems allow you to calculate one side using the lengths of the other two. In this scenario, however, only one side is provided. Good luck as you attempt to solve this riddle, with the solution outlined below...
Visualizing the Problem
The triangle serves as a visual aid for this problem, but solving it requires some algebraic manipulation. By applying the Pythagorean Theorem, we can establish that b² + 19² = c². Since 19² equals 361, we have b² + 361 = c². Our goal is to discover two perfect squares that differ by 361.
To achieve this, we will examine the gap between consecutive square numbers—specifically, the squares of n and n + 1.
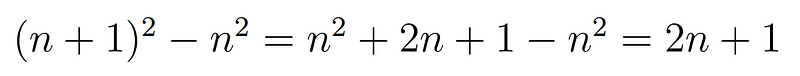
Calculating the Difference
The difference between these squares is given by the formula 2n + 1. By selecting a suitable n, we can adjust this expression to equal any odd number. Our objective is to set the equation 2n + 1 = 361, thereby identifying the value of n that leads to this outcome.
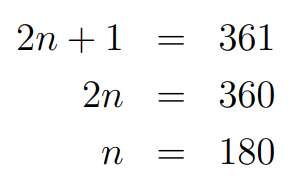
Identifying the Values
Utilizing the formula for consecutive square differences, we discover that 181² - 180² equals 361. Thus, we can conclude that 180² + 19² = 181². This calculation yields our values for b and c: with c as the hypotenuse, we find b = 180 and c = 181. Therefore, our Pythagorean triple is (19, 180, 181).
Challenge Yourself
Challenge 1: Given that 19² represents the difference between two consecutive squares, is it possible for it to also be the gap between another pair of square numbers? In other words, is this solution unique?
Challenge 2: Why does a Pythagorean triple with a hypotenuse of 6 not exist?
For more engaging puzzles like this, be sure to check out my Substack!
Chapter 2: Pythagorean Insights
In this video, titled "Pythagoras Twisted Squares: Why Did They Not Teach You Any of This in School?", viewers will explore intriguing concepts related to Pythagorean triples and their applications in mathematics.
The second video, "Pythagorean Theorem II (Visual Proof)", provides a visual demonstration of the Pythagorean Theorem, making complex ideas more accessible and easier to understand.