Understanding Perpendicularity in Polynomials and Their Angles
Written on
Chapter 1: The Concept of Angles in Vector Spaces
In the vector space ( mathbb{R}^n ), we have a clear understanding of angles and perpendicularity, defined through the dot product, which can be represented mathematically as follows:
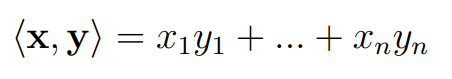
When the dot product of vectors ( x ) and ( y ) equals zero, it indicates that they are perpendicular. Conversely, the dot product reaches its maximum when both vectors point in the same direction. This visual interpretation of angles can be easily understood in two-dimensional (( mathbb{R}^2 )) and three-dimensional (( mathbb{R}^3 )) spaces. The dot product also provides a useful formula for determining the angle between two vectors in ( mathbb{R}^n ):
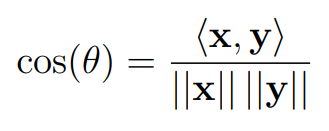
Here, ( ||.|| ) denotes the magnitude of each vector. The dot product exemplifies a scalar product, denoted by angle brackets, which allows us to measure angles in vector spaces even when traditional notions of angles might not apply.
Section 1.1: Understanding Polynomial Spaces
The set of real polynomials ( mathbb{R}[x] ) functions as a vector space over ( mathbb{R} ). Its constituents are polynomials with coefficients that are real numbers, such as ( x^2 + ?x + 1 ) and ( x^? - x^2?? ). Due to the endless nature of polynomial powers, ( mathbb{R}[x] ) requires an infinite basis to encompass all its elements. The most apparent basis is ( {1, x, x^2, x^3, ldots} ), allowing any polynomial in ( mathbb{R}[x] ) to be expressed as a unique sum of these basis elements.
However, this isn't the only basis available for ( mathbb{R}[x] ), which is primarily why mathematicians prefer orthogonal bases. An orthogonal basis is characterized by each basis vector being perpendicular to every other basis vector except itself. Such bases simplify many mathematical operations, making them favorable for various applications, from graphs to scaffolding.
Now, to identify orthogonal polynomials in ( mathbb{R}[x] ), we first need to establish a scalar product. Let's define this concept before breaking it down further.

In ( mathbb{R}[x] ), we can multiply elements, which is a unique feature among vector spaces. We exploit this by integrating the product of two polynomials. The variables ( a ) and ( b ) restrict the polynomial's domain, ensuring inputs are numbers greater than ( a ) and less than ( b ) for a finite integral. Thus, we integrate their product over the interval ([a, b]).
Next, we introduce ( w(x) ), known as the weight function, allowing us to control the contribution of each section of the interval ([a, b]) to the scalar product. This approach resembles the dot product, where each polynomial functions as a mapping of numbers in ([a, b]) to another value, paralleling a vector with infinitely many entries.
Let's illustrate how to find orthogonal polynomials through an example. Consider ( a = 0 ) and ( b = 1 ) with a uniform weight function, ( w(x) = 1 ). Our scalar product now appears as follows:
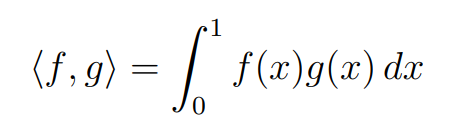
Assuming ( f(x) = x ), we aim to find a quadratic polynomial orthogonal to ( f(x) ) with respect to our scalar product, expressed as ( <x, ax^2 + bx + c> = 0 ). We focus solely on ensuring orthogonality, allowing us to scale the polynomial to be monic and reducing our variables to ( <x, x^2 + ax + b> = 0 ). Now, let's carry out the calculation:
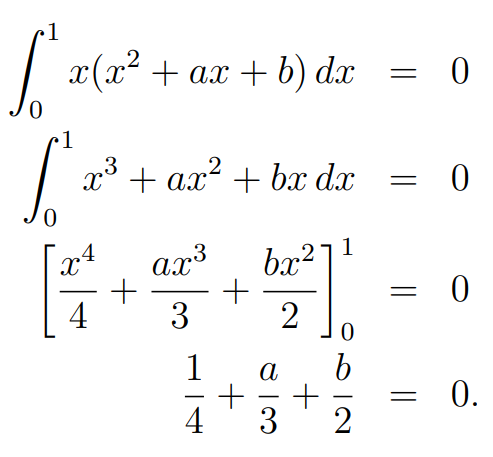
This calculation permits any values of ( a ) and ( b ) that satisfy the equation, leading us to choose ( a = 1 ) and ( b = -7/6 ). Consequently, our quadratic becomes ( x^2 + x - 7/6 ).
Let's visualize these two orthogonal polynomials over the interval ([0, 1]):

This visualization confirms their perpendicularity! The integrated product yields:
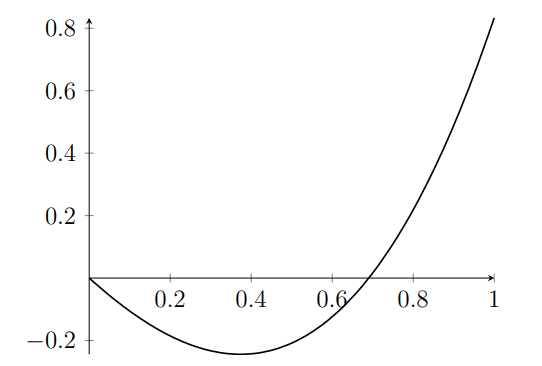
The areas above and below the x-axis appear balanced, aligning with our expectation of a zero integral over ([0, 1]).
Section 1.2: The Gram-Schmidt Process
Given the mathematical preference for orthogonal bases, it’s no surprise that there exists a method to convert any vector space basis into an orthogonal one. This technique, known as the Gram-Schmidt process, will not be elaborated upon here, but its application to the basis of ( mathbb{R}[x] ) is noteworthy.
The Gram-Schmidt process not only orthogonalizes the basis but also normalizes it, ensuring each new basis vector has a length of one. For ( mathbb{R}[x] ) and our scalar product, this results in the following expression for a new basis polynomial ( f(x) ):
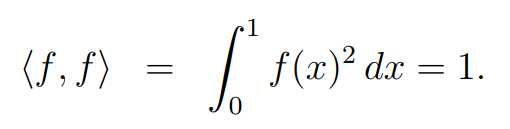
Applying the Gram-Schmidt process to the obvious basis ( {1, x, x^2, x^3, ldots} ) yields the first four polynomials as follows:
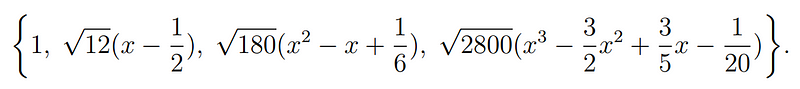
Applications: In approximation theory, large matrix-vector equations are computed to find optimal polynomial approximations for functions. These matrices map ( mathbb{R}[x] ) to itself, and employing an orthonormal basis simplifies these matrices to the identity form, facilitating easier solutions. This is particularly beneficial, as calculators utilize Taylor series or Padé approximations rather than directly knowing exponential or trigonometric functions.
I hope you found this exploration of angles between polynomials enlightening.
Challenge: Find a linear polynomial that is orthogonal to ( x^2 - 9 ) with respect to our defined scalar product.
Chapter 2: Exploring Orthogonal Polynomials through Video Resources
The first video titled "What Are Orthogonal Polynomials? Inner Products on the Space of Functions" delves into the foundational concepts of orthogonal polynomials and their applications in mathematical contexts.
The second video titled "What Are Orthogonal Polynomials? | Differential Equations" provides insights into the connections between orthogonal polynomials and differential equations, enhancing the viewer's understanding of these mathematical constructs.