Introduction to Matrix Inversion

This article builds upon the concepts outlined in “Gaussian Elimination Algorithm in Python,” presenting a technique for calculating the inverse of a matrix through row reduction. For a foundational understanding, refer to the linked article below.

A tutorial detailing how to solve systems of linear equations via Gaussian elimination in Python.

Background on Inverse Matrices

In "Fundamentals of Matrix Algebra | Part 2," the concept of inverse matrices is explored. It's essential to remember that not every matrix can be inverted. A matrix must be square (n×n) and possess a non-zero determinant to qualify for inversion.

A comprehensive guide on implementing basic matrix algebra operations using Python.

When a matrix is multiplied by its inverse, the result is the Identity Matrix, denoted as I, as demonstrated in Equation 1.

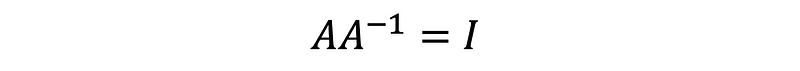
As an illustration, consider the 3×3 matrix A represented in Equation 2.

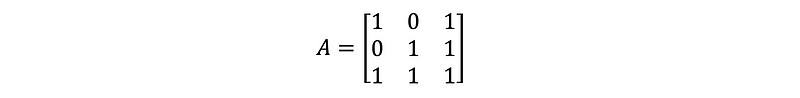
Equation 3, which substitutes variables in Equation 1, is also relevant.

The next step is to compute the unknown A⁻¹.

Matrix Inversion Algorithm

To begin, construct an augmented matrix derived from the components of Equation 3. This augmented matrix consists of A combined with I, as shown in Equation 4.

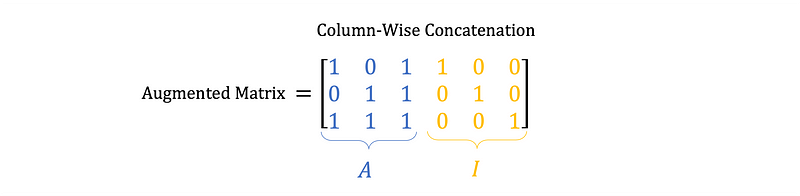
To find the inverse matrix, apply row operations to this augmented matrix. By performing a Gaussian elimination-style procedure, A will be transformed into its reduced row echelon form (rref), which simultaneously modifies I into A⁻¹.

In summary, the process involves:

1. Converting A into rref, thus transforming A into the identity matrix.

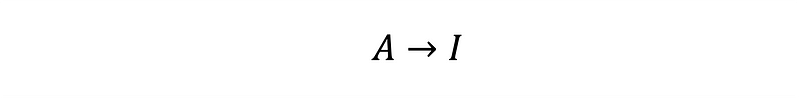
2. Executing the same row operations on I, which yields the inverse matrix A⁻¹.

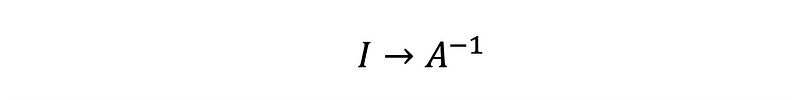
Step-by-Step Example

Figure 1 illustrates the sequential operations required to convert the first three columns of the augmented matrix into rref.

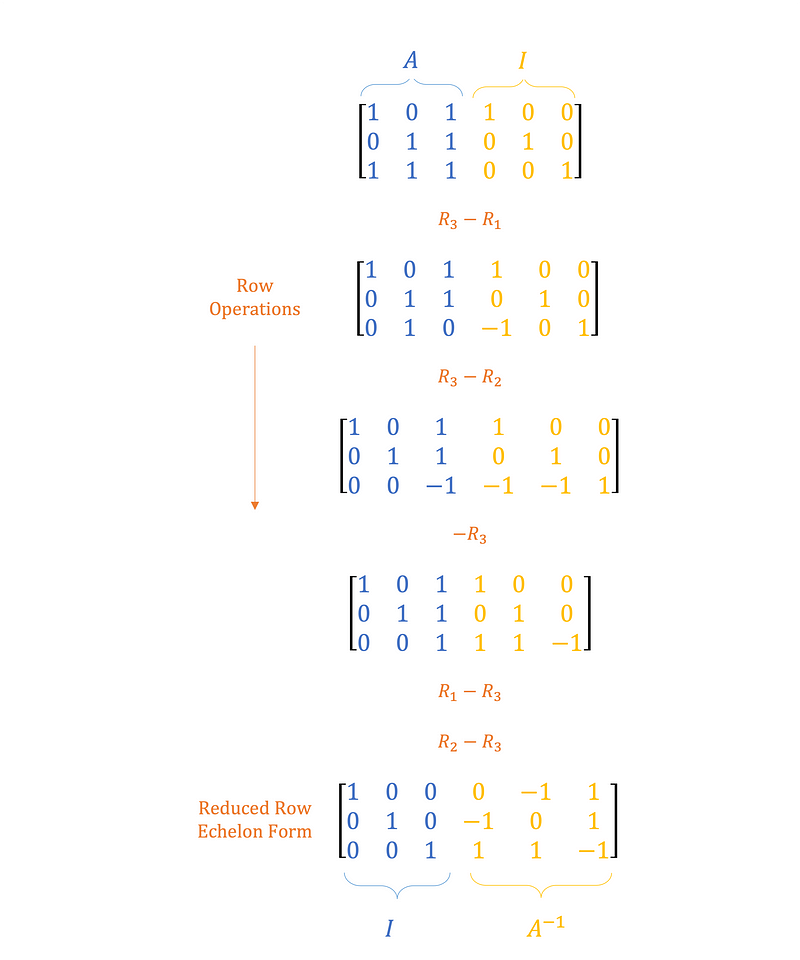
As anticipated, A morphs into the identity matrix, while I changes into the sought-after inverse matrix.

Python Implementation

With the Gaussian elimination algorithm already coded in Python, only minor adjustments are necessary to derive the inverse. Define A from Equation 2 as a NumPy array.

Additionally, create a new variable I that mirrors the shape of A.

Next, generate the augmented matrix using NumPy’s column-wise concatenation function.

Without considering certain edge cases, the following code snippet represents a basic implementation of the row operations needed to compute A⁻¹.

In contrast to the Gaussian elimination algorithm, the critical alteration in the code is that it continues beyond reaching row-echelon form, advancing to reduced row echelon form. Thus, instead of merely iterating below the pivot, it also manipulates the rows above it. Executing the script yields results consistent with those shown in Figure 1.

Performance Results

This algorithm is applicable to any number of invertible matrices, regardless of size. The code in Gist 5 demonstrates how to create a random square matrix in NumPy.

Analyzing the runtime of this custom algorithm compared to the NumPy equivalent reveals a significant speed advantage for NumPy. The code in Gist 6 illustrates a straightforward way to measure the execution times.

In fact, NumPy can be over a second faster in inverting the matrix, and this time difference will only grow as matrix dimensions increase.

Conclusion

This article has provided an essential method for calculating the inverse of a matrix using foundational concepts from matrix algebra. Utilizing the theoretical matrix algebraic method alongside the provided Python code will deepen your understanding of this operation. However, for practical applications, it's advisable to leverage optimized libraries like NumPy, which are designed for efficiently calculating inverse matrices.

For more insights into Python programming, engineering, and data science, feel free to explore my other articles.

Find all Python code in Gist 7.

References

[1] Matrix Algebra for Engineers — Jeffrey R. Chasnov

The first video demonstrates how to calculate the inverse of a matrix using NumPy, providing a practical guide to this essential operation.

The second video explores finding the inverse of a matrix from scratch using Python programming, detailing the step-by-step process involved.