Section 1.1: Understanding Prime Numbers

To establish whether a number ( n ) is prime, we must confirm that it has no divisors other than 1 and itself. If ( n ) can be divided evenly by another number, then ( n ) is either a prime or composed of prime factors. Thus, we only need to verify divisibility against prime numbers.

If we find a prime factor larger than the square root of ( n ), it implies that ( n ) also has a corresponding smaller factor. Therefore, we only need to check for divisibility by primes up to the square root of ( n ). Let's proceed with an example: let ( n = 871 ).

Step 1: Estimate the square root of ( n ). In our case, we can start with 30. Since ( 30^2 = 900 ) which is greater than 871, it's prudent to overestimate to ensure we don't overlook any potential factors.

Step 2: Check the basic primes first—2, 3, and 5.

• For divisibility by 2, look at the last digit; it should be even.
• For 3, sum the digits of ( n ); if the result is divisible by 3, then so is ( n ).
• For 5, the last digit should be either 0 or 5.

Step 3: Now we move on to the next prime, which is 7. To check for divisibility by 7, we can adjust ( n ) by adding or subtracting 7 until we reach a multiple of 10. If ( n ) is divisible by 7, then the resulting multiple of 10 will also be divisible by 7.

Let's illustrate this with our example of 871:

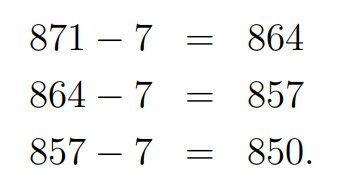
After subtracting 7 from 871, we get 864. Dividing this by 10 gives us 86.4, which simplifies our calculations.

We can then see that 85 is not divisible by 7, confirming that ( n = 871 ) is not divisible by 7.

Next, we’ll test for 11:

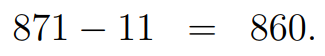
Dividing ( n ) by 10 yields 86, which is not a multiple of 11.

Now, let’s check divisibility by 13. Adding 13 is often quicker than subtracting:

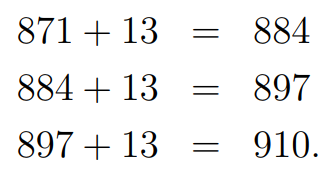
Dividing by 10 results in 91, which is indeed divisible by 13. This means that ( n = 871 ) can be expressed as ( 13 times 67 ), establishing that it is not a prime number.

Finding that ( n ) is not prime is sufficient, but we can also ascertain how many times 13 fits into 871. Since ( 7 times 13 = 91 ), we can multiply ( 70 times 13 = 910 ). Therefore, we see that we need to subtract 3 from 70 to arrive at 67.

Thus, ( 871 ) is not prime, and we can express it as ( 871 = 13 times 67 ).

Extension: Using this methodology, try determining whether the following numbers are prime: 279, 331, and 1223.