What Exactly is a Helix?

To understand this, we first need to clarify the idea of self-congruent curves. Consider two circular arcs sharing the same curvature. If we slide one arc along the other, they will align perfectly. This characteristic is known as self-congruent curves.

When we apply this concept in three dimensions, it leads to practical applications like curved sheaths for walking sticks or scabbards for swords. A prime example of such a three-dimensional self-congruent curve is the helix.

Visualize a cylinder with vertical lines drawn along its surface parallel to its axis. A circular helix is a curve that wraps around this cylinder, maintaining a consistent angle with the vertical lines on its surface.

This definition covers the essential aspects of a circular helix. Other variations exist, but for our purposes, this explanation suffices. Now, let’s explore a captivating property of helixes.

A Unique Characteristic of the Helix

Recall that a helix is classified as a self-congruent curve. By manipulating the helix's angle, we can see that lower-dimensional self-congruent curves manifest as the angle of a circular helix approaches certain limits.

If the angle nears zero, the circular helix becomes a straight line. Conversely, as the angle approaches 90°, the helix resembles a circle. In both scenarios, the self-congruency characteristic remains intact.

The Helix Puzzle: Problem Overview

The task presented by the Helix Puzzle is quite straightforward. Imagine a cylinder that stands 16 centimeters tall, around which a circular helix is wrapped. This helix maintains a constant angle of 60° with the vertical lines on the cylinder's surface. Your objective is to calculate the length of the helix.

This may seem like a brief description, but it invites you to think creatively and approach the problem from different angles.

Spoiler Alert:

If you prefer a more challenging experience, feel free to tackle the puzzle independently. However, if you'd like to simplify your approach, consider the hint provided below. Once you've attempted the puzzle, feel free to continue reading for a detailed exploration of the solutions.

Hint:

Utilize the Pythagorean theorem to approach this puzzle.

How to Approach the Helix Puzzle

Let’s begin with the hint. How can the Pythagorean theorem be integrated into this problem? We know it involves right-angled triangles.

So, what is the connection between right-angled triangles and helixes? The answer becomes clear with a bit of visualization. Picture a right-angled triangle with its base aligned with the base of the cylinder. The height of this triangle must equal the height of the cylinder (16 cm).

By wrapping this triangle around the cylinder, we find that the hypotenuse corresponds to the helix we want to determine. The only requirement is that this hypotenuse forms a 60° angle with the vertical lines on the cylinder’s surface.

Now we can move forward in solving our puzzle, as illustrated below:

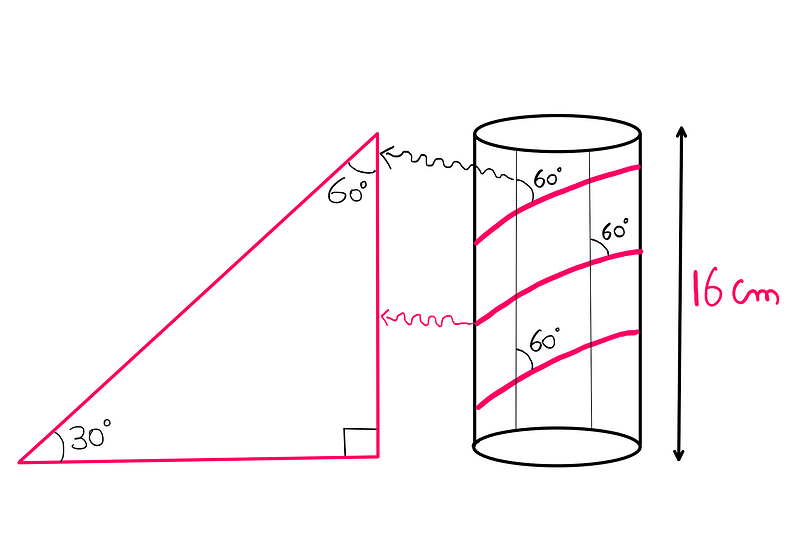
Thus, by applying the Pythagorean theorem and calculating the length of the hypotenuse, we also find the length of the circular helix:

As a result, the length of the circular helix is double the height of the cylinder. Since the cylinder's height is 16 cm, the length of the helix comes out to be 32 cm.

Reference and Credit: Martin Gardner.

Further Reading Suggestions: Explore related puzzles like "Can You Really Solve This Rep-Tile Puzzle?" and "How To Casually Guess Numbers After Dice Throws?"

If you wish to support my work as an author, consider contributing on Patreon.

You can read the original essay here.

Watch the video titled "HELIX PUZZLE SOLUTION" for a detailed walkthrough of the problem and its solution, enhancing your understanding of geometric concepts.

Check out "E14 - SOLUTION - Helix by Hanayama Cast Puzzles" for an engaging exploration of the Helix Puzzle and its intricacies.