Exploring the Wave Nature of Matter in Physics Education
Written on
Chapter 1: The Intersection of Matter and Waves
The connection between matter and waves, particularly at the level of elementary particles, is a fundamental concept that warrants earlier introduction in physics education. This relationship was first proposed by the French physicist Louis de Broglie in 1924. Despite its elegance, the idea faced skepticism at the time and continues to be presented only later in the physics curriculum. Numerous attempts to bridge the gap between classical mechanics and quantum studies have not yielded success, and vice versa. In simpler terms, it is challenging to deduce the wave-like characteristics of a large mass merely by observing it. This essay aims to uncover the missing link that can clarify this relationship.
The integration of general relativity with quantum mechanics is a vibrant area of research. We will explore a basic thought experiment that illustrates classical mechanics while extending our comprehension of both realms.
Consider a stone with a defined radius, r meters, elevated to a height of H meters above the ground, ready to be dropped. Sir Isaac Newton's equation, H = 0.5gt², predicts the relationship between height and time. To introduce wave properties, we will assume that the height H corresponds to the radius of a sinusoidal wave with a wavelength, λ:
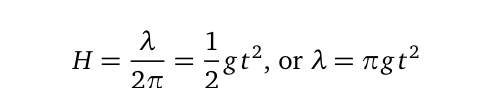
This assumption leads us to analyze the relationship between instantaneous positions and velocities during free fall. Instead of tracking the stone’s velocity (v = gt), we will observe the wave characteristics produced—specifically, the wave's speed (u) and frequency (f). This approach allows us to formulate conclusions and generalize the phenomenon based on our thought experiment.
The relationship between the wavelength and wave speed can indeed be used to predict Newtonian gravitational potential and free fall times. The following equation summarizes this relationship:
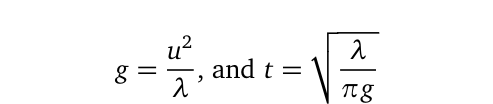
By substituting the wavelength λ into this equation, we can estimate the wave's linear and angular speeds, as well as its frequency and period.
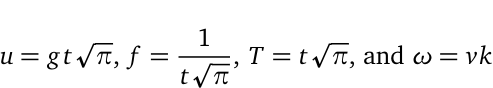
In classical wave theory, frequency is treated as an independent variable, measurable as a vibration. Interestingly, the product of frequency (f) and wave speed (u) yields a precise value for Newtonian gravity (g), expressed as g = uf.
Transitioning to General Relativity
While the previously discussed methodology may appear simplistic, its implications are profound when applied to the context of general relativity. Wave properties can transform into electromagnetic phenomena. For instance, planets perpetually "fall" around their stars, adhering to Newton's law of universal gravitation. The corresponding wavelength can be described as a function of Schwarzschild radius:
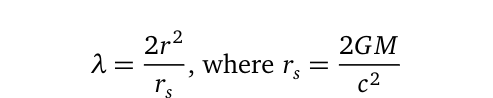
Here, r denotes the radius of the object in question (for Earth, approximately 6,375,087.55 m), influenced by the gravitational field of the sun. The calculations for frequency and velocity are purely electromagnetic and are linked by the equation λf = c, where c is the speed of light in a vacuum. The retarded time of the wave, tᵗ, becomes a known constant:
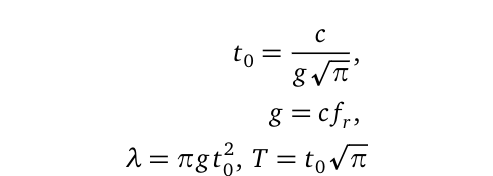
In this equation, T represents the wave's period, while fᵗ refers to a constant set of ultra-low frequencies (ULF) for substantial celestial bodies. These frequencies are presumed to be dependent on position rather than the matter itself, despite both occupying the same coordinates in spacetime as per Einstein's theory.
Notably, these frequencies can be measured independently. Thus, directing a radar at the location of a massive body should yield scalar vector frequencies. When multiplied by the speed of light, this results in the gravitational acceleration of the body as shown in the equation above.
A quick review of nearby planets indicates that Jupiter has the highest radio frequency at 77.05 nHz, while Pluto has the lowest at 2.335 nHz. Earth's frequency sits at 32.71 nHz. Multiplying these frequencies by c yields gravitational values of g = 23.1, 0.7, and 9.80665 m/s² for Jupiter, Pluto, and Earth, respectively.
Understanding black holes also benefits from this approach. Non-rotating black holes have radii equal to the Schwarzschild radius by definition. Thus, we can state confidently that the equivalent wavelength for a Schwarzschild black hole is simply 2r_s, or twice the radius.
The solution to the metric tensor that fully characterizes an object in a gravitational field can be derived by letting the wavelength recede by a factor of Δλ = λ - r. Substituting λ from the Schwarzschild equation into this difference yields a solution to Einstein's field equations:
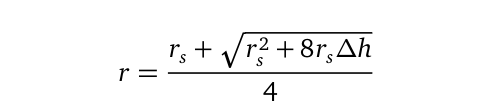
This equation indicates that an object is classified as a black hole if Δλ ≥ r. The mass of the resulting black hole, should it form due to gravitational collapse, is given by:
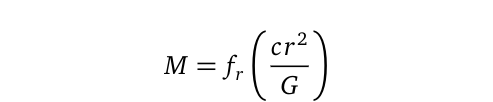
In this framework, the classical question of what constitutes "waving" does not arise, as matter itself behaves as a wave, akin to how elementary particles are defined in the context of de Broglie-Compton relations at the subatomic level.
To validate the earlier equation, consider calculating gravitational potential energy assuming H = R, the radius of a traveling sinusoidal wave. You would use E = mgR instead of E = mgH, leading to the conclusion that these two expressions are equivalent because R = H = λ/2π. Moreover, if no energy is lost, gravitational potential energy will completely convert to kinetic energy:
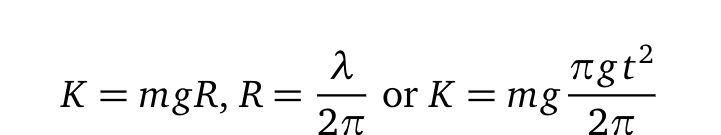
We recognize that the object's speed v = gt, leading to K = mv²/2, as established in classical mechanics.
Conclusion
This exploration has transformed a straightforward abstraction of motion equations into a comprehensive depiction of the interplay between matter and waves within a gravitational field. We have extended this generalization to resolve previously perplexing topics in both classical mechanics and general relativity. Generally, matter tends to emit a wave that extends significantly beyond its own dimensions and can be analyzed similarly to classical waves. This essay thus provides a more accessible perspective for new learners in physics, presenting matter as indistinguishable from waves, with consistent mathematical correlations paralleling the behavior of objects in classical mechanics.
Chapter 2: Video Insights
The first video titled "Properties of Matter Waves - Noise Reduced" offers an in-depth explanation of the characteristics of matter waves, emphasizing their significance in understanding quantum mechanics.
The second video, "Properties Of Matter Wave Or De Broglie Wave," delves into the foundational principles of the de Broglie hypothesis, illustrating the wave-particle duality of matter.
References
¹ Feynman, R.P., 2006. QED: The Strange Theory of Light and Matter. Princeton University Press.
³ Eppelbaum, L., Kutasov, I. and Pilchin, A., 2014. Applied Geothermics (pp. 99–149). Springer Berlin Heidelberg.