Chapter 1: Can π Serve as a Data Repository?

Is it feasible to utilize π as a medium for storing movies? The idea of π being a data archive has been a topic of curiosity. The question arises: does π truly encompass all conceivable information, including films and articles?

Over the years, various claims have emerged regarding π's origins, often romanticized rather than scientifically grounded. These claims frequently reference concepts of infinity or the belief that its decimal expansion contains every possible sequence of numbers.

While intriguing, these assertions lack conclusive proof. The normality of π has yet to be demonstrated, although many mathematicians are optimistic that it is indeed normal based on current research trends. If we accept this premise, we can assert that the digits within π are uniformly distributed, suggesting that any sequence of numbers can be found within its decimal representation. This leads us to ponder: could our favorite movie be encoded within π?

Yes, it is conceivable! By representing both the film and π as binary strings, we could potentially locate the bit sequence corresponding to the movie within π.

However, if π indeed contains every film, article, and piece of data ever created, why aren't we actively searching for these elements within its digits? The answer lies in the concept of compression.

When we seek a bit sequence within π, intending to record the position of its first occurrence, this process acts as a form of compression. The goal is to conserve space by storing just the position of the sequence instead of the entire string. For this to be efficient, the position (a number) must be smaller than the sequence itself; otherwise, we would be using more space than necessary.

Let’s delve into the mathematics behind this.

Section 1.1: Understanding the Math Behind π

To determine the average position of a sequence {X₁, X₂, X₃, …} within π, we need to assess whether this position is less than the length of the sequence itself. The relevant theorem states:

If {X₁, X₂, X₃, …} represents a series of independent and identically distributed random variables within a set S of m elements, the expected first occurrence time of the contiguous subsequence is defined recursively by:

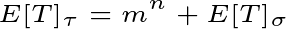
For instance, consider searching for the sequence "456456" within π.

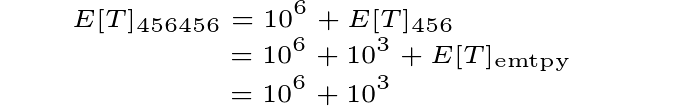
This sequence can be expressed using just six digits, but its position within π requires seven digits (1001000). Here, the sequence "456456" appears at position 1023671. Thus, storing its position demands more space than the sequence itself.

Furthermore, we should consider that:

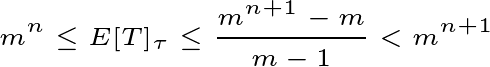
This illustrates an exponential growth in space requirements as the subsequence length increases.

Conclusion: The Practicality of Storing Movies in π

While theoretically feasible to "store" a movie within π, assuming it is a normal number, the practicality of searching for a sequence and merely noting its position proves inefficient. Statistically, saving the position often requires more space than directly storing the sequence, and this requirement increases exponentially.

These observations apply not only to π but also to any normal number.

Chapter 2: Practical Applications of Raspberry Pi for Media

Discover how you can transform your Raspberry Pi into a wireless Plex movie streaming server. This video provides step-by-step guidance on setting up your own media server.

Explore whether a Raspberry Pi can effectively function as a NAS media server. This video evaluates its performance and capabilities.