Section 1.1: Differential Operators as Matrices

To illustrate this, consider that many functions possess associated Taylor series. From complex analysis, we understand that any holomorphic function is also analytic, which means it has a power series expansion. This property also applies to numerous real functions, allowing us to define a mapping L: ℋ → ℝ^∞. This mapping assigns a power series to a vector made up of its coefficients.

By establishing this mapping, we can correlate each function with a vector of coefficients. Notably, the addition of two functions equates to the addition of their corresponding coefficient vectors. Although we are dealing with an infinite-dimensional vector space, we will not delve into the complexities of that concept here.

With this understanding, let's explore how the ordinary differential operator manifests in the vector space.

As we differentiate the function from earlier and reapply the mapping L, we quickly observe the existence of a unique matrix that transforms a function's coefficient vector into that of its derivative.

This leads us to define our infinite matrix as D. To solidify this theory, let’s examine a simple example.

Subsection 1.1.1: Example with a Polynomial

Consider the polynomial f(x) = 3x³ + 2x² + x + 5. By applying the mapping L, we derive its coefficient vector and differentiate using the matrix D. Upon returning to the original function, we utilize the inverse of L.

Notably, D², when interpreted as a matrix product, corresponds to differentiating twice when applied to a coefficient vector. This is represented by the following formula:

In general, we have:

where the first row's non-zero entry appears in the n+1'th column. Importantly, D⁰ = I, the identity matrix, and adjusting the exponent shifts the non-zero diagonal accordingly.

When we raise D to the power of -1, we note that the n!/0! term disappears, yielding:

This gives us our integral operator with a constant of 0—though it is not the inverse of D.

Let’s denote this matrix as J. We find that DJ = I, yet JD ≠ I, which aligns with the fundamental theorem of calculus: differentiating an integral returns the original function, while the reverse yields a shifted function of the form f(x) + c.

Section 1.2: The Translation Operator as a Matrix

Now, let's explore the concept of raising a number to an operator. To do so, we first need to define the arithmetic of operators. Consider two operators, T and R, which take functions as inputs. Their sum and product can be defined based on the resulting function transformations.

For instance, we can express (T + R) f(x) = T f(x) + R f(x).

Similarly, we define the product as applying one operator after the other:

(TR) f(x) = T (R f(x)).

Now, let’s examine the operation of raising e to the differential operator d/dx, utilizing the power series representation for e^x. We'll begin with the ordinary differential operator d/dx, recalling the Taylor series results.

The Taylor expansion of an analytic function f can be represented as a power series centered at x. Additionally, the Taylor series for e^x centered at 0 is:

To apply the aforementioned operator, we must analyze its effect on a function. We combine the definitions of operator addition and multiplication with the Taylor series expansion.

Consequently, we have:

where S f(x) = f(x+1). It can be demonstrated using the binomial theorem that:

Armed with this intriguing outcome, let’s identify the corresponding matrix for this shift operator.

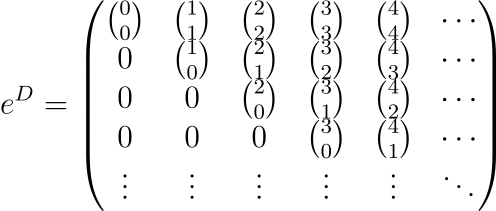
Here, we find that D^n/n! can be elegantly expressed using binomial coefficients, making the summation of these matrices straightforward since we simply add them at each entry level.

By employing our previous matrix calculations and discerned patterns, we arrive at:

where the diagonal consists solely of 1s, presenting a clearer pattern.

Section 1.3: Applications of the Translation Operator

This operator serves as a fascinating combinatorial object, facilitating the expansion of a function f(x+a) in terms of its power series centered at 0. For example, applying this to a polynomial yields:

The matrix e^D can thus be represented as a 3 × 3 matrix, with all other coefficients being 0. This aligns with the expected results.

This representation corresponds to the binomial theorem, extending beyond mere functions of the form (x + y)^n = S_y x^n.

Moreover, we can define the operator U: f(x) → f(-x) as the matrix:

This allows us to formulate a specific symmetry operator as a combination of these matrices, which I discussed in a previous article:

This equips us with linear algebra tools to delve deeper into the subject.

As we wrap up, I encourage your thoughts and feedback below. I aimed to introduce this combinatorial perspective of calculus, and I hope it sparks further ideas for exploration.

Thank you for taking the time to read this. If you enjoy content like this, consider joining the Medium community for full access to articles.