# Understanding the Essence of Matrix Determinants
Written on
Chapter 1: The Fundamentals of Matrix Determinants
In the realm of linear algebra, the concept of determinants often remains a mystery until one dives deeper into its geometric interpretation. Understanding this aspect can profoundly alter your perspective on the topic.
Image by Author (marcelmoos.com)
Reflecting on my high school experience, I found linear algebra to be particularly captivating. It equipped me with the tools to address extensive systems of linear equations while providing a geometric lens through which to view these problems, making the entire process much more intuitive.
Initially, my education focused on matrix determinants merely as numerical values to be calculated, without delving into their deeper significance. It wasn't until my university studies that I truly appreciated the elegance of determinants. Once I grasped their geometric meaning, I couldn't help but wonder why this enlightening concept wasn't introduced in high school—it's accessible and thought-provoking.
In mathematics, the primary question should not be how to compute something; rather, it should be, “What exactly is it?” Only after establishing this foundation should we inquire, “Now that we understand it, how can we calculate it?” Take derivatives, for example. Most of us can summarize them simply: given a function, its derivative represents its slope or rate of change. This straightforward definition is both powerful and freeing, allowing us to comprehend the essence of derivatives, independent of the specific function or its dimensionality.
No educator would present derivatives to students by saying, "Given a function, a derivative is merely another function, and here's how you compute it." Yet, similar approaches seem prevalent when it comes to matrix determinants. Defining determinants through their geometric significance is just as impactful as conceptualizing derivatives as slopes rather than merely functions.
Section 1.1: Determinants and Their Geometric Nature
Before we delve into determinants, let's briefly revisit their context: matrices. A matrix functions as a grid of numbers, representing a linear transformation that takes a vector as input and produces another vector as output.
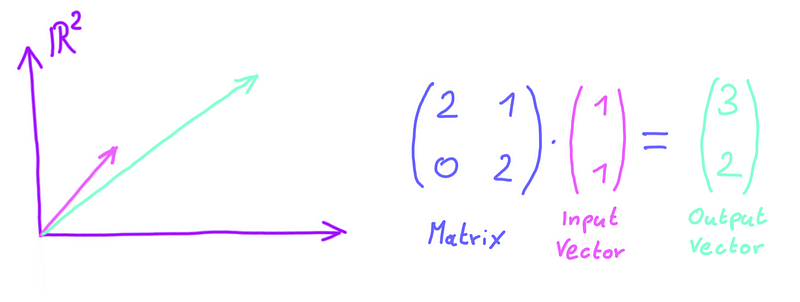
Instead of thinking of a matrix as transforming just one vector, consider it as capable of transforming multiple vectors simultaneously:
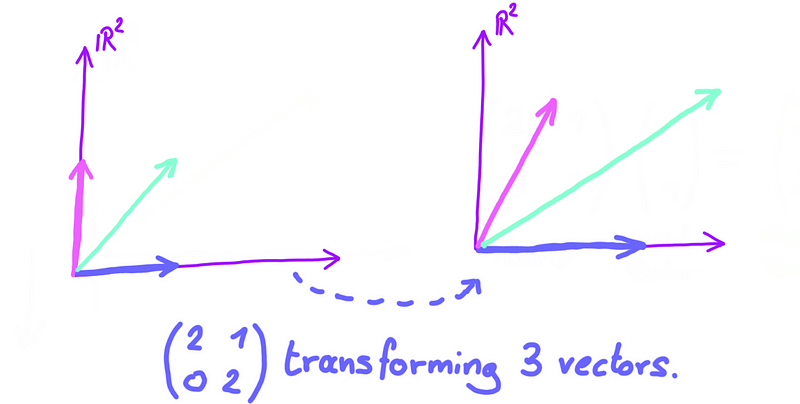
Notice how the chosen matrix appears to stretch space. Regardless of the area selected in the input space, the transformation seems to enlarge it. This scaling effect is precisely what the determinant quantifies!
The determinant of a matrix indicates the factor by which areas are scaled by that matrix. Since matrices are linear transformations, knowing the scaling factor for a single area suffices to determine the scaling factor for all areas. Consider this example:
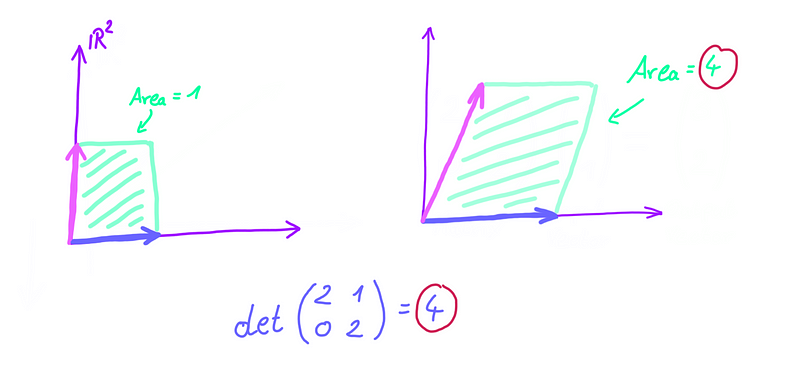
The rectangle formed by the pink and blue unit vectors initially has an area of 1. After the matrix transformation, this rectangle morphs into a parallelogram with a base of 2 and a height of 2, resulting in an area of 4. Hence, our matrix scales areas by a factor of 4, meaning the determinant is 4. Fascinating, isn't it?
However, there's an important caveat: determinants can also be negative. If we start with an area of 1 and scale it by a negative factor, the area would become negative—an absurdity. So how do we interpret this geometric definition in the context of negative determinants? The solution is simple: if a matrix has a negative determinant, say -2, areas are scaled by 2, with the negative sign indicating a reversal in orientation.
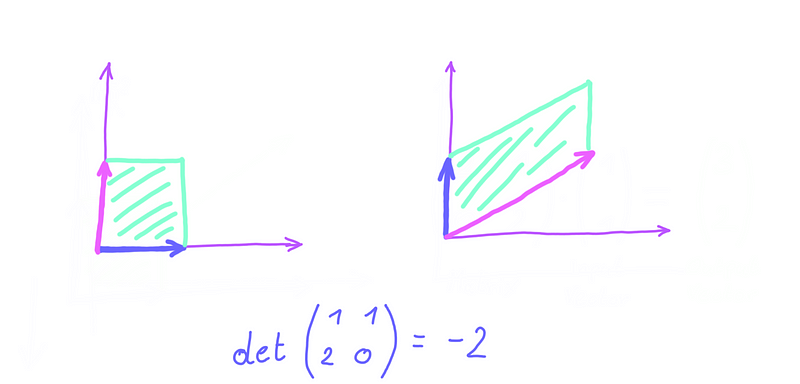
Notice how, after the transformation, the blue vector shifts from being on the right of the pink vector to the left. This illustrates the concept of orientation reversal. Consequently, the determinant is -2, reinforcing the idea that the determinant of a matrix signifies the signed factor by which areas are scaled. A negative determinant indicates a reversal of orientation.
All our discussions have focused on two dimensions. It's challenging to illustrate higher-dimensional graphs, but the geometric interpretation of determinants remains applicable across dimensions. In three-dimensional space, the determinant represents the signed scaling factor for volumes, and in even higher dimensions, it pertains to hypervolumes.
Chapter 2: The Power of Understanding
The first video, The Determinant | Chapter 6, Essence of Linear Algebra, delves into the critical nature of determinants in linear transformations, providing insights that enhance our understanding of this concept.
The second video, Matrices | Determinant of a Matrix (Part 1) | Don't Memorise, further explores the computation and significance of determinants, reinforcing the geometric interpretation discussed earlier.
Equipped with this geometric understanding of determinants, we can tackle problems that would otherwise be daunting. For instance, consider the fact that if a matrix's determinant equals 0, it is deemed non-invertible. This means the transformation represented by the matrix cannot be undone.
If we view a matrix with a determinant of 0, it suggests that the matrix scales all areas to 0, implying that the entire space is compressed into a lower dimension. For example, a transformation in two dimensions could collapse the space to a line or point, making reversibility impossible.
At this juncture, we can take pride in our progress. We've introduced matrix determinants as factors that scale areas and have validated a well-known property of matrices without needing to calculate determinants. Yet, the question of computation is secondary at this point.
Feel free to connect with me on LinkedIn for any inquiries or thoughts you might have. If you enjoyed this piece, consider subscribing to my newsletter at marcelmoos.com/newsletter.