Understanding the Area of Intersection Between Two Circles
Written on
Chapter 1: Visualizing the Intersection
What would the graph representing the intersection look like?
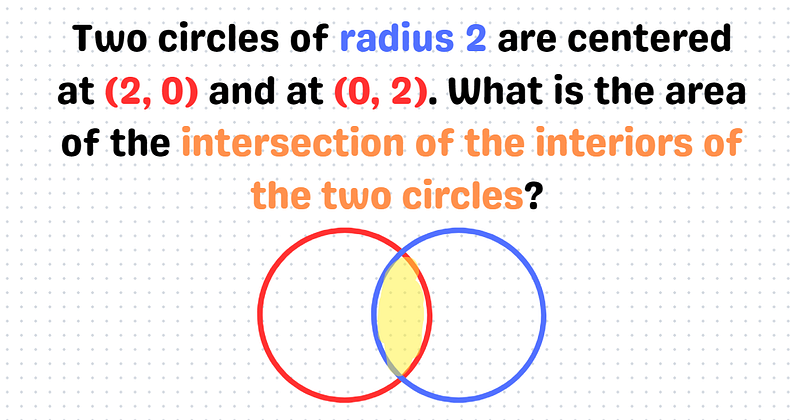
The intersection of two circles resembles a Venn diagram; however, the graph we need to create deviates slightly from that concept. Are you ready to merge your knowledge of geometry and algebra to find the answer? I suggest pausing here to grab some pen and paper. Once you're prepared, continue reading for the solution!
Solution
The two circles each have a radius of 2, positioned at centers (2, 0) and (0, 2), respectively. Let’s plot that data.
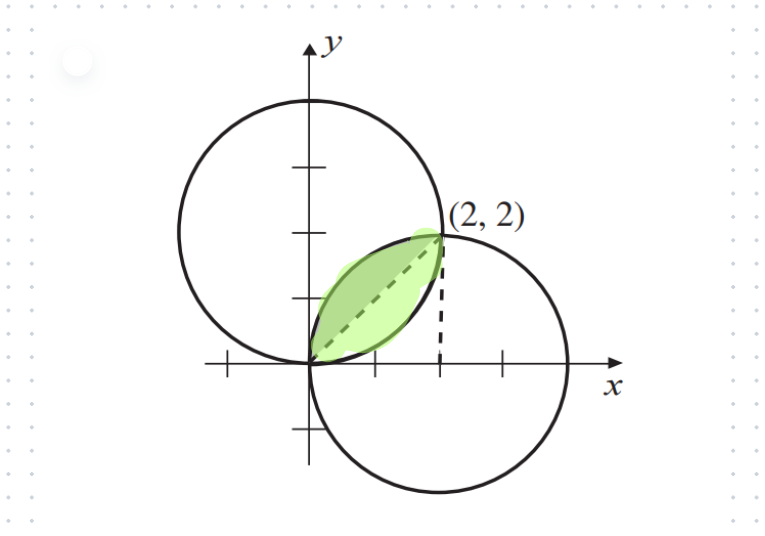
Do you know how to verify that these circles intersect at the points (0,0) and (2,2)? Our main goal is to determine the shaded area of overlap. We can conceptualize half of this area as the region obtained by subtracting an isosceles right triangle (with leg lengths of 2) from a quarter section of one of the circles.

Now, the area of the quarter circle can be calculated as ( frac{1}{4} pi (2)^2 = pi ). The area of the triangle is ( frac{1}{2} (2)^2 = 2 ). Hence, the area of half of the region is ( pi - 2 ). Therefore, the total area we seek is double that value.
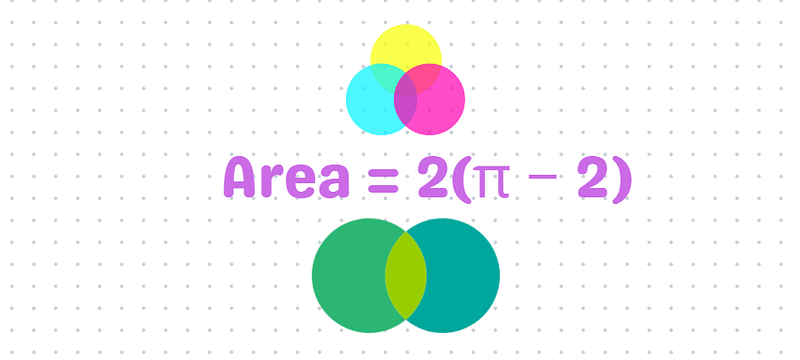
And that’s how we arrive at our solution.

Photo by Amber Wolfe on Unsplash
Isn’t this fascinating? I’d love to hear your thoughts on this problem. Feel free to share your insights in the comments below!
Math Puzzles
Explore the best math puzzles available on Medium, covering topics like Algebra, Geometry, Calculus, Number Theory, and much more.
Bella’s Weekly Math Games
Join our exciting 48-hour weekly math competition!
If you want to stay updated whenever I publish new content, please sign up. Thank you for your support!
Thank you for reading! If you found this article helpful, please give it a clap.

If you’d like to show your appreciation, consider buying me a coffee. Your generosity greatly supports my writing and personal endeavors. Happy problem-solving, Bella! If you wish to connect or chat, don’t hesitate to reach out!